- Startseite
- Schwarzes Loch - der "Fotobeweis"
-
Mit dem Zwillingsparadoxon ausgetrickst
- "Zirp" von LIGO

Walter Orlov
|
 |
Der Übergang von Lorentzscher Äthertheorie zur Einsteinschen Relativitätstheorie generierte ein Problem. Bei Lorentz ist die Zeitdehnung immer real. Die Anwendung der Relativität bedingt aber eine symmetrische Betrachtung, die oft als wechselseitige Zeitdilatation bezeichnet wird. Selbstverständlich betrifft dasselbe die Längekonraktion. Bewegen sich zwei Beobchter relativ zu einander, kann jeder von ihnen behaupten, dass beim Anderen die Uhr langsamer geht bzw. der Andere abgeplattet aussieht. Um zur bleibenden Verlangsamung der Zeit zu gelangen, braucht man einen komplizierteren Vorgang, als nur eine Momentaufnahme. Das sogenannte Zwillingsparadoxon ist die richtige Wahl. Die Idee lieferte Einstein selbst, obwohl an ein Paradoxon hätte er offensichtlich noch nicht gedacht:
"Befinden sich in A zwei synchron gehende Uhren und bewegt man die eine derselben auf einer geschlossenen Kurve mit konstanter Geschwindigkeit, bis sie wieder nach A zurückkommt, was t Sek. dauern möge, so geht die letztere Uhr bei ihrer Ankunft in A gegenüber der unbewegt gebliebenen um ½t(v/V)2 Sek. nach." (Link)
Später kam das Zwillingspaar ins Spiel: Ein der Zwillinge unternimmt die Reise durch das Weltall und als er zurückkommt, ist sein Bruder um einiges älter als er selbst. Menschliche Schicksale machten die Geschichte aufregend... Aber achten wir lieber auf das Wort "Paradoxon" nicht, sonst beginnen wir vorangenommen zu denken. Es gibt hier kein Paradoxon. In diesem Fall ist das nur eine Wortkombination, die absichtlich eingeführt wurde. Man wolle vermutlich das Publikum unterhalten, nicht weiter.
Wie ich hier erfahren dürfte, lässt sich das Zwillingsparadoxon wahrscheinlich am einfachsten mit Hilfe vom relativistischen Dopplereffekt darstellen. Vorteilhaft kann man dabei Beschleunigungs- bzw. Bremsphasen ganz außer Acht lassen.
Entfernen sich Sender und Empfänger voneinander, ändert sich die empfangene Frequenz elektromagnetischer Welle folgendermaßen: f = f0[(1 – v/c)/(1 + v/c)]1/2, wobei f0 die Frequenz elektromagnetischer Welle im Bezugssystem des Senders ist und v die Geschwindigkeit ist, mit der sich Sender und Empfänger relativ zueinander bewegen. Um mit einfachen Zahlen später zu rechnen, wird für ein anschauliches Beispiel oft v = 0.8c gesetzt. So ergeben sich folgende zwei für uns relevante Frequenzen:
Sender und Empfänger entfernen sich voneinander: f = f0/3;
Sender und Empfänger nähern sich einander: f = 3f0.
Jeder Zwilling bekomm einen Sender, der mit einer festen Frequenz f0 = 1 Hz die Funksignale sendet. Er dient stellvertrettend für eigene Uhr des jeweiligen Zwillings. Man kann die Funksignale zählen und somit gleich sehen, wieviel Sekunden bei anderem Zwilling vergangen wurden.
Ein der Zwillinge unternimmt die Reise zum nächsten Stern. Proxima Centauri ist ca. 4.2 Lichtjahre entfernt. Einfachheitshalber berechnen wir alle Beschleunigungs- bzw. Bremsphasen mit 0 Sekunden. Er startet mit v = 0.8c. Im Bezugssystem der Erde erreicht er den Stern in 4.2 Lichtjahre / 0.8c = 5.25 Jahren. Zusammen mit dem Rückflug ergeben sich 10.5 Lichtjahre. Für den auf der Erde gebliebenen Zwillig vergehen also 10.5 Jahre. Weil sich der reisende Zwilling relativ zum erdgebundenen Zwillig die ganze Zeit mit 0.8c bewegt hat, vergehen bei ihm wegen der Zeitdehnung 10.5 Jahre (1 – v2/c2)1/2 = 6.3 Jahre. Aber, wie es oben schon erwähmt wurde, ist die Zeitdehnung wechselseitig. Der reisende Zwilling würde die Formel für die Zeitdehnung nicht für sich selbst, sondern für seinen Bruder auf der Erde einsetzen. Ja, er darf das auch gern machen, trotzdem wird das Ergebnis dasselbe sein... Das belegt die Rechnung mit dem relativistischen Dopplereffekt.
Während der Hinreise zum Stern entfernen sich die Zwillinge voneinander. Daher beträgt die Frequenz der empfangenen Funksignale wie oben berechnet nur ein Drittel von der Referenzfrequenz: f0/3. Das sehen zwar beide Zwillige, aber verschieden lang. Für den erdgebundenen Zwilling gibt es zwei Zeitabschnitte. Es ist die Zeit, die der reisende Zwilling braucht, um den Stern zu erreichen. Wir haben das bereits berechnet: 5.25 Jahre. Aber der erdgebundene Zwilling sieht das nicht sofort, die Nachricht erreicht ihn erst 4.2 Jahre später ( = der Abstand zwischen Erde und Stern geteilt durch die Lichtgeschwindigkeit). Insgesamt sind es 9.45 Jahre, multipliziert mit ein Drittel der Referenzfrequenz, ergeben sich 3.15 Jahre f0 Funksignale. Da wir vorher absichtlich f0 = 1 Hz gewählt haben, beträgt die Dauer zwischen den Funksignalen exakt 1 Sekunde eigener Zeit. Deshalb entspricht die Zahl der Funksignale von 3.15 Jahre f0 genau der vergangenen eigenen Zeit von 3.15 Jahren.
9.45 Jahre nach dem Start sieht der erdgebundene Zwilling seinen Bruder zurückkehren. Die empfangene Frequenz ist dabei dreimal höher als Referenzfrequenz, aber bis zur Ankunft bleiben nur 10.5 Jahre – 9.45 Jahre = 1.05 Jahre übrig. Als Folge ergeben sich wieder 3.15 Jahre f0 Funksignale.
Halten wir also fest: Aus der Sicht des auf der Erde gebliebenen Zwilling hatte der reisend Zwilling sowohl für die Hinreise als auch für die Rückreise jeweils 3.15 Jahre gebraucht, insgesamt 6.3 Jahre. Das ist nicht so weit überraschend, weil wir dasselbe Ergebnis vorher einfach mit der Formel für die Zeitsdehnung bekommen haben. Interessant ist eben anders: Was sieht der reisende Zwilling?
Wegen der Längekontraktion erscheint dem Reisenden die Flugstrecke bis zum Stren um Faktor (1 – v2/c2)1/2 = 0.6 kürzer: 4.2 Lichtjahre 0.6 = 2.52 Lichtjahre. Deshalb passiert er sie in 2.52 Lichtjahre / 0.8c = 3.15 Jahren. Sein Zwillingsbruder auf der Erde lag wohl richtig mit seiner Rechnung. Aber wie hat er aus der Sicht des reisenden Bruders inzwischen gealtert? Der reisende Bruder multipliziert seine Reisedauer mit der empfangener Frequenz, die einem Drittel der Referenzfrequenz gleicht, und bekommt 3.15 Jahre f0/3 = 1.05 f0 Funksignale. Sein Bruder auf der Erde hat tatsächlich langsamer gealter. Das wechselseitige Zeitdehnung hat sich bewahrt... aber nur bis zu diesem Zeitpunkt. Nach der Umkehr empfängt der reisende Zwilling sofort das Dreifach der Referenzfrequenz und das resultiert sich in 3.15 Jahre 3f0 = 9.45 Jahre f0 Funksignale. Zusammen sind es 10.5 Jahre f0 Funksignale.
Die beiden Zwillinge sind sich also einig: Der zurückgebliebene Bruder altert schneller als der reisende. So wird der Bann der wechselseitigen Zeitdehnung gebrochen. Die Verlangsamung der Zeit wird zur Realität!
Die Betrachtung ist einwandfrei. Die Anwendung des relativistischen Dopplereffekts bedingt automatisch die Anwendung der Formel von der Zeitdilatation von jedem Zwilling für die Bestimmung des Zeitverlaufs bei seinem Bruder. Nichtdestotrotz altern sie verschieden schnell.
Auch wenn die Rechnung stimmig ist, fühlt man sich irgendwie ausgetrickst. Das kennen wahrscheinlich viele und fragen nach, denn gleich wird schon die Erklärung geboten: Während sich der Zwilling auf der Erde die ganze Zeit in Ruhe befindet, wechselt der reisende Zwilling bei der Umkehr das Inertialsystem und, überhaupt, er wird mehrmals hin und her beschleunigt. Dadurch wird er quasi intuitiv zum echten Reisenden. Aber wie wird all das in der Rechnung berücksichtigt? – Gar nicht! Angewendet wird nur die Geschwindigkeit des Reisenden, anders, etwa die Synchronisation der Uhren, wird nicht verlangt. Das wechseln der Inertialsysteme bedingt keine zusätzlichen Erscheinungen, die in der Rechnung extra berücksichtigt werden sollten. Und beschleunigungsphasen rechnen wir mit 0 Sekunden.
Ferner können wir gleiche Beschleunigungsphasen sowie das Wechseln des Inertialsystem beim zurückgebliebenen Zwilling einfügen. Z.B., beide Zwillinge können gleichzeitig vom Erdorbit starten. Einer wird aber gleich danach am Rande des Sonnensystems bremsen und dort auf Rückkehr seines Zwillingsbuders warten. Am Ende der Reise werden sie dann gemeinsam zur Erde fliegen. Dadurch ergibt sich zwar eine kleine Korrektur, aber sie ist eben so klein, dass die Zahlen in obiger Rechnung auf gleiche Werte wieder gerundet werden können.
Den Unterschied macht die Längekontraktion. Aus der Sicht des reisenden Zwillings verküzt sich die Fluglinie Erde – Stern um den Faktor (1 – v2/c2)1/2. Egal wie weit und wie lange gereist, bräuchte er immer weniger Kilometer zurückzulegen, als im Bezugssystem der Erde bestimmt wurde, und kehrt deshalb zur Erde immer jünger als sein zurückgebliebener Bruder zurück.
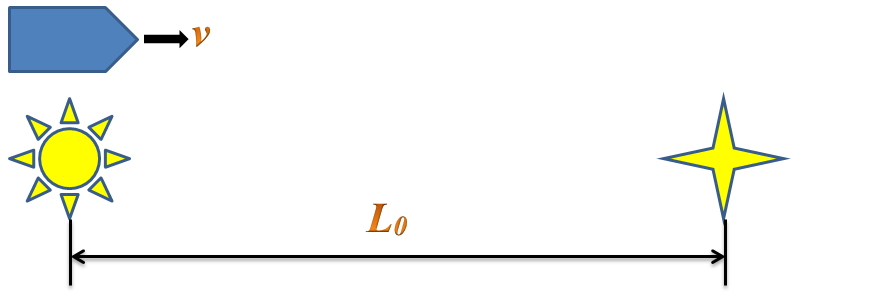
Warum hat aber der erdgebundene Zwilling keine Gelegenheit die Formel für die Länge-Kontraktion anzuwenden? – Weil die Entfernung bis zum Flugziel im seinem Bezugssystem definiert ist. Und das ist der Trick!
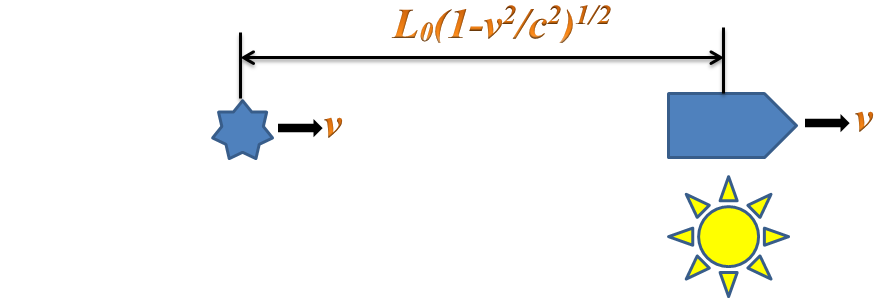
Ferner, nach der Ankuft, lenkt das Gravitationsfeld der Sonne dem Meteroiden von seinem geradlinigen Kurs ab, kehrt ihn um, sodass er mit gleicher Geschwindigkeit zurückfliegt. Der reisende Zwilling macht einen ähnlichen Umkehr-Manöver, nachdem er 4.2 Lichtjahre zurückgelegt hat, auf selbe Art oder mit Hilfe von den Racketentriebwerken. Der Abstand zwischen reisendem Zwilling und Meteroiden bleibt deshalb immer gleich. Sie sind relativ zueinander stets in Ruhe.
Siehe auch Zeitdehnung und Einsteins Relativität
Kostenlose Homepage erstellt mit Web-Gear
Verantwortlich für den Inhalt dieser Seite ist ausschließlich der Autor dieser Webseite. Verstoß anzeigen