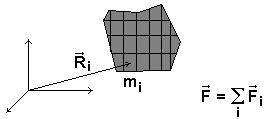
|
Das Gravitationsgesetz von Newton arbeitet mit den Punktmassen. Hat man mit einem ausgedehnten Körper zu tun, kann der Körper zu mehreren kleinen Massen mi geteilt werden. Danach misst man Abstand Ri zu jedem Massenstückchen, das schon annähernd als Punkt betrachtet werden kann, berechnet die Kraft Fi und zum Schluss summiert vektoriell die Beiträge:

Von besonderenr Bedeutung ist die Ortung des Schwerpunktes. Allgemein benutzte Formel ist aber aus dem Hebelgesetz geleitet und eigentlich nur für homogenes Feld gültig. Anders ausgedruckt, findet man auf diese Weise den Massenmittelpunkt, weil als Gewichtfaktor nur die Masse verwendet wird:
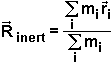
Wollen wir tatsächlich den Schwerpunkt finden, dann müssen wir schon Gravitationskraft ins Spiel setzen. Aus dem Gravitationsgesetz geleitet darf gesuchte Formel folgend aussehen:
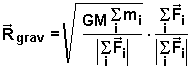
Im Allgemein können sich Massenmittelpunkt und Schwerpunkt an derselben Stelle nicht befinden. Als Beispiel finden wir Massenmittel- und Schwerpunkte für einen Stab mit ß-Liniendichte im Gravitationsfeld einer Außenmasse, wie es auf nächstem Bild gezeigt ist.
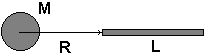
Massenmittelpunkt vom Stab
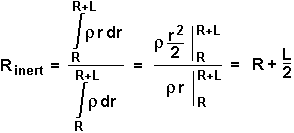
liegt also gerade im Zentrum des Stabes, woran wir eigentlich keinen Zweifel gehabt haben. Jetzt ist aber der Schwerpunkt an der Reihe.
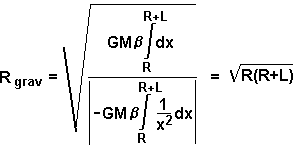
Wenn man die Zahlen in die Formeln einsetzt, sieht man, dass der Schwerpunkt näher der Quelle des Gravitationsfeldes liegt als Inertpunkt. Die Verschiebung ist nicht von der Größe der Außenmasse abhängig, aber von der Entfernung von ihr.
Es wäre natürlich interessant zu wissen, ob in radialsymmetrisch verteilten Massen Massenmittelpunkt und Schwerpunkt tatsächlich denselben Aufenthaltsort haben, wie es allgemein vermutet wird. Ziehen wir eine Kugelobefläche mit dem Radius r in Betracht, deren Zentrum in Entfernung R von der Außenmasse M liegt.
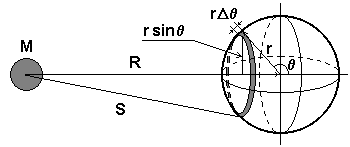
Nach der Abbildung ist die Masse eines Ringes
![]()
µ ist die Flächendichte
Berücksichtigt, dass aus symmetrischen Gründen sein Massenmittelpunkt auf Achse liegen soll, berechnen wir
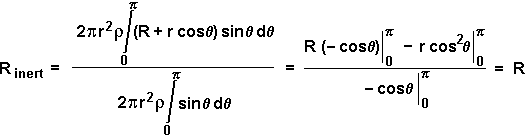
Also, der Massenmittelpunkt befindet sich gerade im Zentrum der Kugelschale.
Schwerpunkt zu finden, ist ein wenig komplizierter. Erst müssen wir berücksichtigen, dass die Kraft senkrechte, symmetrische Teile hat, die einander kompensieren; somit ist nützlicher Rest entsprechend um Faktor
![]()
gemindert. Ganz roh sieht unsere Formel so aus
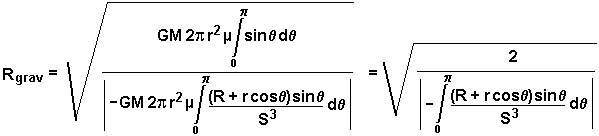
Hier haben wir noch mit zwei Variablen zu tun. Um zu einer zu wechseln, führen wir ein paar Tricks durch. Für die Entfernung darf gelten
![]()
Durch die Differenzierung können wir das Wechselsatz für die Variablen gewinnen
![]()
Und außerdem ohne Differenzierung
![]()
Daher
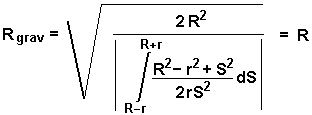
Massenmittelpunkt und Schwerpunkt der Kugeloberfläche befinden sich, also, auf demselben Platz und zwar gerade im Zentrum der Kugeloberfläche. Das muss offensichtlich auch für massive Kugel gelten, etwa für Planeten und Sterne.
Kostenlose Homepage erstellt mit Web-Gear
Verantwortlich für den Inhalt dieser Seite ist ausschließlich der Autor dieser Webseite. Verstoß anzeigen